Inspired largely by Chris Fenton’s Turbo Entabulator, and to some degree by Charles Babbage’s legacy, I started work on a rod computer.

The rod logic uses a completely different mechanism from the difference engine and the Turbo Entabulator.  Many people have constructed basic rod logic gates from Legos or other mechanical contrivances, but most of what I can find on Google is just single gates or an assembly of a relatively small number of gates.  I did find one very admirable effort by Robert Baruch at designing and building a larger scale system with many rods.

Also worth mentioning as prior art is a paper by Ralph C. Merkle that discusses rod logic with the goal of developing a MEMS device that might one day achieve higher density and efficiency than today’s electronic computers.

To get things started, I constructed a proof-of-concept prototype to test the feasibility with moderately sized pieces.  I also wanted to test a particular method for resetting the rods.

Merkle’s design focuses on a mechanism where the rods are reset by running the entire mechanism in reverse, which is important for minimizing energy dissipation.  I had wanted something more akin to regular gates, where information only propagates forward through the network and can feed back into itself.

Within my design I call the input and sensing elements ‘flags’ and ‘pins’ respectively.  If the extended position is considered ‘true’ and the blocked position is considered ‘false’, then each rod computes a NOR function of the perpendicular rods above and below.  Depending on the location of the flag, each input rod may block an output rod in either position, or both (not that useful) or neither.  The output is then true only when none of the input flags block the pins.

The problem with resetting occurs if a flag does not block a pin and the pin moves past the flag.  Then if the flag subsequently blocks the pin while the pin is still extended, the pin is stuck on the far side of the flag.  This prevents the rod from computing anything until the sequence is reversed in order to get the pin out from behind the flag.  With a large number of interacting rods this could be a difficult puzzle all by itself.

To accommodate the resetting and feedback, all rods have three positions instead of two.  Two of the positions correspond to the logical ‘true’ and ‘false’, and the third position is a ‘reset’ position where there are no flags to impede the movement of orthogonal rods.  In the diagram below the blue rods show the three positions.  The dark blue rectangles symbolize where the flags would be and the small orange squares represent the pins.  The left and middle blue rods represent a binary 1 and 0, and the blue rod on the right represents the reset position where the orange rod is not blocked.

Each rod has a forward direction, where pushing the rod will, through one or more pins, detect the presence or absence of flags.  The backward direction moves the rod to the reset position which deactivates any flags and will always allow the dependent rods to move.  This turns out to work nicely with four phases that are pushed in sequence.  The diagram below shows an arrangement with rods oriented north (blue), west (orange), south (green), and east (yellow).
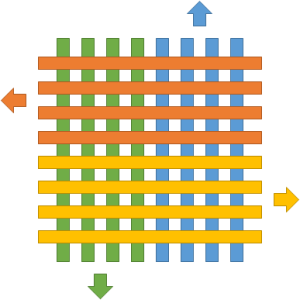Here at the blue/orange intersections, the blue rods can have flags and the orange rods have pins, such that the blue rods are input for the orange rods.  The orange rods are then input to the green rods, meaning that at the orange/green intersections, the orange rods have flags and the green rods have pins.  Likewise the green rods are input for yellow and yellow are input for blue.This arrangement is especially nice when it comes to resetting the rods.  If blue and green rods are pushed north together, the blue rods will compute based on the position of the yellow rods, and the green rods will reset, since they are pushed backwards.  Then if the orange and yellow rods are both pushed west, the orange rods will compute based on the position of the blue rods and the yellow rods will reset.  Since the green rods are reset, there will be no green flags to prevent the resetting of the yellow rods.  The problem of pins being stuck past the flags can’t occur because of the sequence of resetting: all the inputs (flags) are reset just prior to resetting the outputs (pins) that depend on them.Here is a demonstration of the cycle with one rod in each direction:

In this instance, the blue/orange (north to west) intersection replicates the value, meaning if the north rod is extended, then it does not block the west rod, and if the north rod is blocked, then it also blocks the west rod.

Three of the intersections are of this propagating type, and one intersection, the east to north intersection, is inverted.  So if the east rod is extended, it blocks the north rod, and if the east rod is blocked, then it does not block the north rod.

Later we’ll have to see how well this scales to dozens of gates or more…